News
October 03, 2021: Branched Flow Special - New Manuscript Published in pNAS!
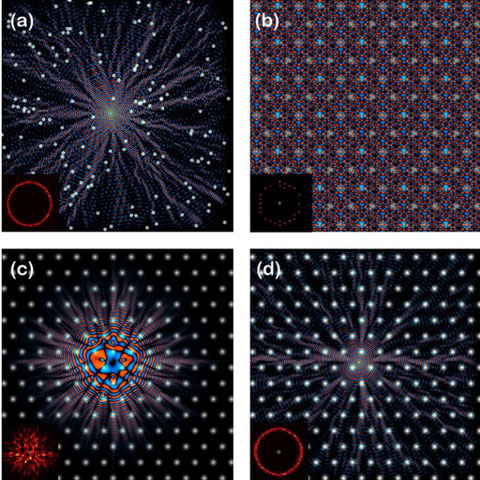
Published in PNAS: A. Daza, E. J. Heller, A. Graf. E RASanen: "Propagation Of Waves in high brillouin zones: Chaotic branched Flow and Stable Superwires"!
Great news! - Our latest research on Branched Flow was published in PNAS
Abstract: We report unexpected classical and quantum dynamics of a wave propagating in a periodic potential in high Brillouin zones. Branched flow appears at wavelengths shorter than the typical length scale of the ordered periodic structure and for energies above the potential barrier. The strongest branches remain stable indefinitely and may create linear dynamical channels, wherein waves are not confined directly by potential walls as electrons in ordinary wires but rather, indirectly, and more subtly by dynamical stability. We term these superwires since they are associated with a superlattice.
Significance: Waves propagating through random media can accumulate in strong branches, intensifying fluctuations and powerful phenomena such as tsunamis. However, branched flow is not restricted to the large scale, and here, we find surprisingly that branched flow is not restricted to random media. We show that quantum waves living in the high Brillouin zones of periodic potentials also branch. Moreover, some of these branches do not decay as in random media but remain robust indefinitely, creating dynamically stable channels that we call superwires. The waves in these stable branches have enough energy to surmount the channel potential and go elsewhere, but classically, nonlinear dynamics keeps them confined within the channel. These results have direct experimental consequences for superlattices and optical systems.


Alvar's Guest Lecture about Branched flow at Harvard Univeristy
Title: Propagation of waves in high Brillouin zones: Chaotic branched flow and stable superwires.
Speaker: Alvar Daza
Duration: 65 min.
Abstract: We report unexpected classical and quantum dynamics of a wave propagating in a periodic potential in high Brillouin zones. Branched flow appears at wavelengths shorter than the typical length scale of the ordered periodic structure and for energies above the potential barrier. The strongest branches remain stable indefinitely and may create linear dynamical channels, wherein waves are not confined directly by potential walls as electrons in ordinary wires but rather, indirectly, and more subtly by dynamical stability. We term these superwires since they are associated with a superlattice.
Waves propagating through random media can accumulate in strong branches, intensifying fluctuations and powerful phenomena such as tsunamis. However, branched flow is not restricted to the large scale, and here, we find surprisingly that branched flow is not restricted to random media. We show that quantum waves living in the high Brillouin zones of periodic potentials also branch. Moreover, some of these branches do not decay as in random media but remain robust indefinitely, creating dynamically stable channels that we call superwires. The waves in these stable branches have enough energy to surmount the channel potential and go elsewhere, but classically, nonlinear dynamics keeps them confined within the channel. These results have direct experimental consequences for superlattices and optical systems.
Great News! The Blochbusters Alvar, Rick, Anton and Esa published a new paper on Branched Flow in the peer-reviewed Journal PNAS.
Did this picture spark your interest? Check out our new article on PNAS and learn all about the science behind this image!

September 26, 2021: First AnimAtions Are Online!

"Branched Flow Boogie"
Watch Branched Flow dancing in the sea of phonons!
Pictures of branched flow show the density of trajectories running over a fixed potential. If the potential evolves in time, so does the branched flow pattern. In this animation, the deformation potential caused by lattice vibrations varies in time, putting the branched flow to dance at the phonon rhythms.
Technical description: The video was made as a concatenation of branched flow pictures for different deformation potential snapshots. For each snapshot hundreds of trajectories were numerically integrated, and the density of trajectories was plotted.
"The awakening of the phonons"
Here you can see that phonon modes awake as temperature rises.
Atoms of a frozen crystal at zero temperature are believed to remain still in their lattice positions. However, as temperature rises, atoms start to vibrate and therefore phonons are created. First, the long-wave phonons appear, since they do not require much energy. Then, for higher temperatures, short-wave phonons accumulate on top of the longer modes. Finally, as temperature increases over the Debye temperature all modes are activated, so no new features appear and simply the population of phonons increases. As a consequence, the peaks grow higher and the valleys get deeper.
Technical description: Using the expression of the deformation potential, we fixed all the parameters (including random phases) and only varied the temperature. All the frames were plotted with the same colour bar revealing how, as the temperature increases, new details appear and the peaks grow higher.


"A SEA OF SOUNDS"
Watch Branched Flow dancing in the sea of phonons!
Pictures of branched flow show the density of trajectories running over a fixed potential. If the potential evolves in time, so does the branched flow pattern. In this animation, the deformation potential caused by lattice vibrations varies in time, putting the branched flow to dance at the phonon rhythms.
Technical description: The video was made as a concatenation of branched flow pictures for different deformation potential snapshots. For each snapshot hundreds of trajectories were numerically integrated, and the density of trajectories was plotted.
August 25, 2021: More new Images!
"Magnetic Focussing"
Description: Magnetic focussing and branched flow compete in shaping the flow of electrons emitted form a quantum point contact into a two dimensional semiconductor crystal subjected to a magnetic field.
Technical details: Simulation of quasiclassical trajectories of electrons in a perpendicular magnetic field in a model potential of the disorder in a semiconductor nanostructure (upper half) and in an idealized model without disorder (lower half).
Read on related research:
>Maryenko D, et al. (2012), "How branching can change the conductance of ballistic semiconductor devices", Physical Review B., May, 2012. Vol. 85(19), pp. 195329.
>Aidala, K. E. et al. (2007), ” Imaging magnetic focusing of coherent electron waves”. Nature Phys 3, 464–468.


"Three to one"
Description: A branched flow generated by a random potential with different characteristic length scales in the horizontal and the vertical direction.
Technical details: The picture shows the density in a two dimensional classical flow emitted from a point source over an anisotropic random potential with a ratio of horizontal to vertical correlation length of 3:1.
Read on related research:
>Degueldre, H. et al (2017), "Channelling of Branched Flow in Weakly Scattering Anisotropic Media", Physical Review Letters., January, 2017. Vol. 118(2), pp. 024301.
"Mixed Bag II”
Description: The interplay of a regular and a random potential creating the precursor of a branched flow. The phenomenon is analogous to the images "RANDOM REFLECTIONS" and "REGULAR BUT STRANGE" which you can find above!
Technical details: The picture shows the ray density in a kick-drift model with (2+1) dimensions after a single kick. The two dimensional kick potential is generated by the product of two sinusoidal functions, a Gaussian and a Gaussian random field.

August 13, 2021: New Images Online!

"Random Reflections"
Description: Surely you have seen the reflections of the sunlight playing on the sides of the boats in a harbour on a sunny afternoon. Or the bright lines of light at the bottom of the sea near the beach. These can be understood as the precursors of branched flow in 3 dimensions. The figure shows the intensity pattern of a bundle of initially parallel light rays after three consecutive such reflections from (or refraction incidents at) random surfaces.
Technical details: The picture shows the ray density in a kick-drift model with (2+1) dimensions after 3 kicks. Each kick is the impulse created by 2-dimensional potential landscape in for of a Gaussian random field. The potential in each kick is distinct but with the same characteristics, i.e. strengths and correlation lengths.
"Regular but Strange"
Description: Regular cousin of a 3-dimensional branched flow. These staggering forms are created by 5 deflections from a regular and localized potential instead of the random potentials creating an “ordinary” branched flow.
Technical details: The picture shows the ray density in a kick-drift model with (2+1) dimensions after 5 kicks. Each kick is the impulse generated by the same 2-dimensional regular potential created by the product of two sinusoidal functions and a Gaussian.


"Mixed bag"
Description: The interplay of a regular and a random potential creating the precursor of a branched flow. The phenomenon is analogous to the images "RANDOM REFLECTIONS" and "REGULAR BUT STRANGE" which you can find above!
Technical details: The picture shows the ray density in a kick-drift model with (2+1) dimensions after a single kick. The two dimensional kick potential is generated by the product of two sinusoidal functions, a Gaussian and a Gaussian random field.
July 21, 2021: New Image Looking for a name!

This new image is looking for a name. What does this look like to you? There are no limits to your imagination! Leave your suggestions in the comments below.
Physically speaking, this is a rendering of a branched flow pattern. It is a different rendering of the exact same data used to produce the image "Landscape".
-
#3
Mustafar (Saturday, 08 October 2022 17:34)
Planet from star wars
-
#2
Victor Newsom (Thursday, 21 October 2021 06:26)
"Lavascape" comes to mind or "Lava Fields"
-
#1
Max (Saturday, 11 September 2021 17:45)
Looks like a magma ocean!
June 14, 2021: NEW IMAGES ADDED TO THE ART GALLERY!
"Green 3"
We called this image “Green 3”, green for Green’s function. A snapshot of 25 quantum explosions, with 25 waves that were tiny dots a moment ago now blowing up because of the Uncertainty Principle. Starting out as dots, each was very certain where it was, which in quantum mechanics means you will have little idea how fast you are going or in what direction. So a moment after they were set free, the 25 quantum waves are caught spreading out, and fast. The thing is, the landscape around each dot is irregular, and differently so for each one, so the waves bend in weird ways. There is another beautiful piece of physics built into this picture: if you look at each wave explosion, the farther you go out from the center, the shorter the wave lengths become. This is because the faster parts of the wave have travelled farther from the center, and in quantum mechanics, faster waves have shorter wavelength. The initial uncertainty in speed is revealed in a large range of positions, with speeds revealed by position later.


"Quantum Storm"
This “storm” is a wave, a quantum electron wave having a tough day, trying to propagate through a metal. It was traveling easily at the top, moving downward, when it encountered some impurities in the metal, and all hell broke loose. The “lucky” parts of the wave have made it, not too badly deflected, to the lowest parts of the cloud, raining down. The parts that got deflected sideways are lagging behind (nearer to the top) - because they have stopped moving down. The parts near the top have been deflected more severely and are lagging even further behind. Near the top are parts of the wave that have retreated backward and are heading up!
The add to the mystery of quantum mechanics, this is a wave for a SINGLE electron, and the brightness give the probability of finding the electron there if you look. So, only theorists like us can “see” the electron like this; if an experimentalist looks for the wave, he/she will just find an electron somewhere, at one spot, in one of the whiteish zones.
The appearance is whiteish because the wave has its positive parts colored blue, and its negative parts colored orange, with hues that are complimentary. The result is white overall, but the colors appear looking closer. There is no white in the picture!
"Landscape"
The freedom we have to display data is enormous, and we do it differently both for artistic reasons and to highlight different aspects of the science. Branched flow, as seen elsewhere on Blochbusters, is a ubiquitous wave and particle phenomenon coming from travel over a smooth but (typically) random landscape. It can also happen traversing a smooth but periodic landscape, as in a crystal. To learn more about this topic click here.

April 05, 2021: New Images added to the Art Gallery!

"Forest in the sea"
Description: A beam of trajectories representing electrons are launched vertically from bottom to top. They are gently deflected by the deformation potential created by the sea of phonons, which is shown in green tones. This image is very different from the traditional pictures of electric resistivity, but branched flow was first discovered in electron diffusion in a 2d electron gas, so it should not be surprising to find it in electron-phonon interactions too.
Technical details: To make this picture we launched parallel trajectories from bottom to top. The dark branches represent the density of classical trajectories evolving in the deformation potential (green tones). We used a symplectic scheme to integrate the trajectories, and the deformation potential, which represents lattice vibrations as coherent state picture of phonons, was computed by adding cosine waves with thermally weighted frequencies and random phases.
"Crossroads"
Description: The picture shows the density of classical trajectories in a square lattice. Despite the periodicity of the potential, the chaotic dynamics can generate branched flow: aperiodic structures arise from regular lattices. In random potentials branches decay exponentially fast from the origin, but in periodic potentials the stable branches (pink tones) can remain stable indefinitely.
Technical details: We ran classical trajectories from the center with the same initial energy and a uniform distribution of angles. The potential in which they evolve is made by bumps arranged in a square lattice. As usual, we employed a symplectic integrator and represented the density of trajectories. Quantum simulations in superlattices (lattice constant much larger than the wavelength) display similar patterns.


"Fire"
Description: Random potentials stretch and fold manifolds creating beautiful patterns. This is a phase space representation of a manifold after undergoing several stages of kick and drift. At this point, many cusp catastrophes have happened, which would translate into branches in real space. The variable rarefaction of the different areas indicate also that some regions can accidentally remain stable after a few kicks.
Technical details: Although it has a deep dynamical interpretation, this picture was made using Photoshop. Initially, a thick horizontal line was made, representing the initial manifold. If we assume that the vertical axis is momentum and the horizontal is position, this situation would correspond to launching parallel trajectories with the same initial momentum in real space. Then, we applied a random wave filter, acting as the kick, followed by a shear deformation, which corresponds to the drift stage in phase space. After repeating these two operations several times this picture was obtained.
March 29, 2021: New Preprint Uploaded on The Arxiv!
“From branched flow to superwires in periodic potentials”
Authors: Alvar Daza, Eric J. Heller, Anton M. Graf, Esa Räsänen.
Waves propagating through weakly refracting media typically accumulate in strong branches. Tsunamis provide a powerful example of this branched flow in the large scale, but this general wave phenomenon affects the quantum realm too. So far, branched flow had only been studied in random media, but here we report for the first time its occurrence in periodic potentials.
One of the major differences of this research with respect to standard investigation of periodic systems is the methodology. Periodic systems such as crystals are usually studied by means of periodic functions, that is, Bloch waves. However, we study the evolution of wave packets in real space by directly integrating the time-dependent Schrödinger equation numerically. Also, we focus into a peculiar regime, where wavelengths are short compared to the potential scale. This would be unphysical for typical crystals, but modern superlattices (such as twisted graphene bilayers) operate precisely in this regime.
Branched flow in periodic potentials comes along with a special feature: dynamically stable channels, which we call superwires (because its relevance to superlattices). In random media, branches can carry high flux density for long distances, but they eventually die. In regular lattices, some branches can remain indefinitely stable. Unlike energetic channels, waves in these stable branches have enough energy to surmount the potential and go elsewhere, but its dynamics keep them confined within the channel. These results have direct experimental consequences for superlattices and optical systems, and they also help understand the role of nonlinear dynamics in branched flow.
Find the full article here.
March 28, 2021: First IMages ONLINE!
"Between Worlds"
Description: The traditional picture for electron diffusion in metals is the Drude model: electrons travel freely until they are kicked in a random direction, and this process happens again and again. This picture shows the electrons (grayscale) diffusing as branched flow, due to the action of the deformation potential created by the sea of phonons (hot colors). We are showing only the highest bumps of the deformation potential, which we believe that contribute more to the branch formation. Could this be a bridge between the traditional Drude model and the sea of phonons picture?
Technical info: the grayscale represents the density of classical trajectories, which were launched from the top left in different angles. We used a symplectic scheme to integrate the evolution of hundreds of these semiclassical paths in the deformation potential. The highest bumps of the potential are represented on top of the trajectories using hot colors.
-
#1
John Ross (Monday, 29 March 2021 17:25)
Beautiful image! Interesting to see how the how the high bumps of the deformation potential affect the branching.
Please share more.
"Blochbusting"
Description: This image can inspire many different things, but technically, this is an electron’s Green function evolving under the action of a periodic potential. In a glimpse, it shows many interesting features. The central part corresponds to the slower components of the electron wave, which lag behind undulating and creating strange patterns. The fast components, where the alternation of blue and yellow shows shorter wavelengths, have spread their branches far from the epicenter. Despite the underlying periodic potential, the electron wave functions display a rich variety of branched flow patterns. Of course, it is possible to assemble such patterns with Bloch waves, but certainly, it is hard to imagine all the complexity that can arise in periodic lattices if one is restricted to periodic waves.
Technical details: The picture was made integrating the the time-dependent Schrödinger equation with a Gaussian wavepacket with zero initial momentum evolving under a triangular potential. The wave lengths involved are shorter than the lattice constant of the potential (high Brillouin zones). The split-operator method was used for the integration, and here we show only the real part of the complex wave function. If we made an energy Fourier transform of this picture (fixed wavelength), we would obtain an eigenfunction.


"Road to Chaos"
This picture captures the phase space mixing of a chaotic map (the so-called standard map). After several stages of stretching and folding the initially ordered colors arrange in a complicated pattern. Although some structures remain stable (circles), we can see the effects of chaos.
Technical details: This picture was made with photoshop. Initially, we had an array of ordered stripes and circles with different colors, and we applied successively filters simulating the kick (periodic distortion) and drift (shear of the picture). This is exactly what the standard map makes in phase space.
March 20, 2021: Recording of Rick's Talk On Branched Flow at Harvard CMSA Is Online!
Title: Branched Flow and Applications
Speaker: Eric J. Heller
Duration: 58 min.
Abstract: In classical and quantum phase space flow, there exists a regime of great physical relevance that is belatedly but rapidly generating a new field. In evolution under smooth, random, weakly deflecting but persistent perturbations, a remarkable regime develops, called branched flow. Lying between the first cusp catastrophes at the outset, leading to fully chaotic statistical flow much later, lies the visually beautiful regime of branched flow.
It applies to tsunami wave propagation, freak wave formation, light propagation, cosmic microwaves arriving from pulsars, electron flow in metals and devices, sound propagation in the atmosphere and oceans, the large scale structure of the universe, and much more. The mathematical structure of this flow is only partially understood, involving exponential instability coexisting with "accidental" stability. The flow is qualitatively universal, but this has not been quantified. Many questions arise, including the scale(s) of the random medium, and the time evolution of manifolds and "fuzzy" manifolds in phase space. The classical-quantum (ray-wave) correspondence in this flow is only partially understood. This talk will be an introduction to the phenomenon, both visual and mathematical, emphasizing unanswered questions
Click here to see the full video.